Mathematics
Welcome to Maths
The maths department is made up of collaborative team of 11 maths specialists that are passionate about teaching their subject. We believe in a maths curriculum that is creative and engaging with the national curriculum at its core. All children are to have access to this curriculum and to make progress in lessons, irrespective of their starting point. Children need to develop the necessary skills to make them “deep thinkers” acquiring maths skills that can be recalled quickly and transferred and applied in different contexts. They need to be able to make rich connections across the areas of maths and use their knowledge in other subjects.
Balcarras Maths Department Endpoints
Maths is the foundation for understanding the world and we want our children to know the purpose behind their learning and to apply their knowledge to their everyday lives.
We expect all pupils to have mastered the topics below by the end of each year.
|
Year 7 |
Year 8 |
Year 9 |
Year 10 |
Year 11 |
|---|---|---|---|---|
|
Multiply Decimals |
Negative Number Calculations |
Standard Form conversions |
Divide decimals |
Standard form calculations |
|
Round to whole number, nearest 10 |
Round to decimal places |
Three rules of indices |
Round to significant figures |
Estimation |
|
Find all factors and multiples of a number |
Write number as product of prime factors |
|
Use PFF to find HCF and LCM |
|
|
Fraction means equal parts, equivalent fractions |
F/D/% conversions |
|
Mixed Number Calculations |
|
|
Measure an angle |
|
Construct perp bisector |
|
|
|
Collect like terms |
Expand single brackets |
Expand double bracket |
Factorise with common factors |
Solve quadratics by factorising |
|
Sub +ve values into expressions |
|
|
Sub negative values into a formula |
Formulae for Cones and Spheres |
|
Angles in Triangle sum to 180 |
Angles in simple polygons
|
Vertically opposite angles |
Angles of regular polygons |
Angle in parallel lines |
|
Find F/V/E for 3d shapes |
Plan of a 3D shape |
Pythagoras- Find hypotenuse |
Pythagoras- Find any side |
SOHCAHTOA |
|
Convert metric units of length |
Calculate Speed given distance and time |
|
|
Speed, Density, Pressure |
|
Ratio- write, equivalent |
Share in a ratio |
Direct Proportion |
Combined Ratio and Proportion problems |
Inverse Proportion |
|
Solve 1 step equations |
Solve 2 step equation |
Solve Equation – unknown both sides |
Solve Equations with brackets and unknowns on both sides |
Solve simultaneous equations |
|
Area of rectangle and triangle |
Diameter is twice radius |
Area and Circumference of a circle |
Area and circumference of semi and quarter circles |
Volume and surface area of a cylinder |
|
Find simple percentages of an amount (non calc) |
Find percentages using a multiplier |
% increase, decrease using multiplier |
Repeated % changes using multiplier |
Reverse percentages |
|
Plot Coordinates in 4 quadrants |
Plot x=a, y = b |
Plot y=mx+c |
Gradient and y intercept |
Plot quadratic equations |
|
Rotate, Reflect and Translate 2D shapes |
Enlargement |
Translate with a vector and combine transformations |
Describe single transformation |
Vector algebra |
|
Averages from discrete data |
Use frequency Tables |
|
Averages from frequency tables |
|
|
Draw Bar Chart |
Dual and Composite Bar Charts |
Scatter diagram and correlation |
Interpret Scatter diagram |
Construct a Pie Chart |
|
|
Find nth term of an increasing arithmetic sequence with positive terms |
nth term for any arithmetic sequence |
generate a sequence given nth term |
Rearrange Formulae |
|
|
|
Represent inequalities on a number line |
Solve linear inequality |
Use inequalities to write an error interval |
|
|
|
Recognise Similar and Congruent shapes |
Find volume of a right prism |
Proof of Congruency |
|
|
Write probability as a fraction |
Probability for independent events |
Probability for dependent events |
Venn Diagrams |
Key to Curriculum maps
|
Basic numeracy |
Geometry |
Sequences |
Probability |
|
Ratios, Proportion, Fractions, Decimals, Percentages |
Statistics |
Algebra |
|
Curriculum map Key Stage 3
|
|
YEAR 7 |
YEAR 8 |
YEAR 9 |
|---|---|---|---|
|
September |
|
|
|
|
October |
|||
|
November |
Factors and Multiples |
|
|
|
December |
|
|
|
|
January |
|||
|
|
|||
|
February |
|||
|
March |
|||
|
April |
|||
|
May |
|||
|
June |
|||
|
|
|||
|
|
|||
|
July |
Curriculum map GCSE (higher level)
|
Septem ber |
Year 10 |
Year 11 |
|---|---|---|
|
October |
||
|
Solving linear equations (including setting up and rearranging formulae) |
||
|
Test and Review |
||
|
November |
Mocks |
|
|
Direct and inverse proportion (both numerical and algebraic approach) |
||
|
December |
||
|
Gradient and area under (non-linear) graphs and graph transformations |
||
|
Test and Review |
||
|
January |
||
|
Revision |
||
| Test and Review | ||
|
Exams |
||
|
Exams |
||
|
Solving quadratic equations (including linear and non linear simultaneous equations) algebraically |
||
|
|
Curriculum map GCSE (Foundation)
|
September |
10 |
11 |
|---|---|---|
|
October |
||
|
|
||
|
November |
||
|
Mocks |
||
|
December |
||
|
January |
||
|
|
||
|
February |
||
|
rearranging equations, graphs of cubic & reciprocal functions |
||
|
Revision |
||
|
|
||
|
March |
||
|
April |
||
|
|
||
|
May |
||
|
Exams |
||
|
June |
||
|
|
Curriculum map A level mathematics
| Pure- 5 hours a fortnight |
| Mechanics- 2 hours a fortnight |
| Statistics- 2 hours a fortnight |
|
|
Y12 |
Y13 |
|---|---|---|
|
Sept |
Indices and Surds |
Proof |
|
|
Quadratics |
Functions and mappings |
|
|
Definitions and Large Data Set |
Correlation |
|
|
Measures of location |
|
|
|
Modelling |
Moments |
|
|
Constant Acceleration |
|
|
Oct |
Equations and Inequalities |
Binomial expansion |
|
|
Graphs and transformations |
Radians |
|
|
Measures of spread |
Probability |
|
|
Constant Acceleration |
Forces and friction |
|
Nov |
Coordinate Geometry |
Trigonometric functions |
|
|
Circles |
Trigonometry and modelling |
|
|
Representing data |
Probability |
|
|
Forces |
Projectiles |
|
Dec |
Algebraic Methods |
Parametric equations |
|
|
Correlation |
Normal Distribution |
|
|
Forces |
Projectiles |
|
Jan |
Binomial expansion |
Mocks |
|
|
Trigonometric ratios |
|
|
|
Trigonometric identities |
|
|
|
Vectors (in mechanics lessons) |
Differentiation |
|
|
Probability |
Application of forces |
|
|
Distributions |
Normal Distribution |
|
Feb |
Mocks |
Differentiation |
|
|
Differentiation |
Numerical methods |
|
|
Hypothesis tests |
Normal Distribution |
|
|
Variable acceleration |
Application of forces |
|
Mar |
Differentiation |
Integration |
|
|
Integration |
Vectors |
|
|
Hypothesis tests |
Revision of Y12 content |
|
|
Variable acceleration |
Vectors in kinematics |
|
Apr |
Exponentials and Logarithms |
Revision and past papers |
|
|
Revision of Y12 content |
Revision and past papers |
|
|
Revision of Y12 content |
Revision and past papers |
|
May |
Revision of Y12 content |
EXAMS |
Curriculum maps Further Maths A level
| Core Pure- 5 hours a fortnight |
| Mechanics- 2 hours a fortnight |
| Statistics- 2 hours a fortnight |
|
|
Y12 |
Y13 |
|---|---|---|
|
Sept |
Complex Numbers |
Series |
|
|
Argand Diagrams |
Methods in calculus |
|
|
Discrete Random Variables |
Negative Binomial Distribution |
|
|
Momentum and impulse |
Momentum and impulse |
|
|
Work, energy and power |
Revision of Y12 collisions |
|
Oct |
Matrices |
Volumes of revolution |
|
|
Discrete Random Variables |
Hypothesis Testing- Geometric |
|
|
Work, energy and power |
Elastic collisions in 2 dimensions |
|
Nov |
Linear Transformations |
Polar coordinates |
|
|
Poisson Distribution |
Probability Generating Functions |
|
|
Elastic Collisions |
Elastic collisions in 2 dimensions |
|
Dec |
Series |
Hyperbolic Functions |
|
|
Proof by induction |
Probability Generating Functions |
|
|
Poisson Distribution |
Revision of Y12 Energy |
|
|
Elastic Collisions |
Revision for mocks |
|
Jan |
Vectors |
Mocks |
|
|
Hypothesis Testing- Poisson |
Methods in differential equations |
|
|
Revision |
Central Limit Theorem |
|
|
Mocks |
Elastic springs (Hooke's law) |
|
Feb |
Volumes of revolution |
Modelling with differential equations |
|
|
Chi-Squared - discrete distributions |
Central Limit Theorem |
|
|
Revision and past papers |
Elastic springs (Hooke's law) |
|
Mar |
Revision and past papers |
Revision and past papers |
|
|
Chi-Squared - discrete distributions |
Quality of Tests |
|
|
Revision and past papers |
Revision and past papers |
|
Apr |
Revision and past papers |
Revision and past papers |
|
|
Chi-Squared - contingency tables |
Quality of Tests |
|
May |
A2 Complex Numbers |
REVISION AND EXAMS |
How is Mathematics organised at Balcarras School?
Year 7 (Y7) is split into two bands with each band containing 3 or 4 tutor groups. For the first half term they are taught as a tutor group. After the October half-term they are put into sets based on their raw KS2 results. If a pupil has not taken KS2 exams or their school does not provide the raw scores, we will use the numeracy test that all pupils sit at the end of the first half term to place them.
Being placed in a lower set does not mean that a pupil is not good at mathematics; it merely reflects their relative position on entry in an intake of nearly 200 pupils. Some pupils and parents find the initial setting to be a worry, especially if a child was one of the best mathematicians in a small primary school but we have found that the only fair way to allocate starting sets is to use the KS2 raw score and rank pupils. It is our aim to stretch and challenge pupils in all sets and at all abilities.
Again this year, pupils who have started at Balcarras in the bottom set in Y7 have achieved grade 8 at GCSE in Y11.
During Y7, changes are made between sets if it is clear that a student is wrongly placed.
All Y7 pupils take a common examination and this, together with performance in class work and homework throughout the year, forms the basis of set allocation for Y8 within two parallel half-year bands.

In Y9 pupils are placed in sets 1-9 as a full year group. In Y10 and Y11 we go back to two parallel half-year bands. Within each band pupils are setted for mathematics based on their exam and class work.

We always enter students into the highest level paper that we believe will maximize their grade in external examinations
Key Stage 3
Follow the kangaroo maths Key Stage 3 Framework for Teaching Mathematics, with a strong mastery approach. In accordance with the National Strategy we aim to develop both mental and written mathematical skills.
The scheme mirrors the requirements of the national curriculum and includes number and algebra, geometry and measures, statistics together with mathematical processes and applications.
Being in smaller set groupings, aided by Teaching Assistants where appropriate, supports the least able.
We set and internally assess KS3 SAT examinations to determine setting for Y10.
GCSE
All students follow a course of study that can lead to a GCSE examination in mathematics. We follow the Edexcel specification and pupils sit three formal examinations at the end of the course. There is no coursework in mathematics. The examinations include elements of ‘functional skills’ and the final grade will be between 9 and 1, with foundation students able to achieve a maximum of a grade 5.
Results are consistently well above the national average and amongst the highest in the county.
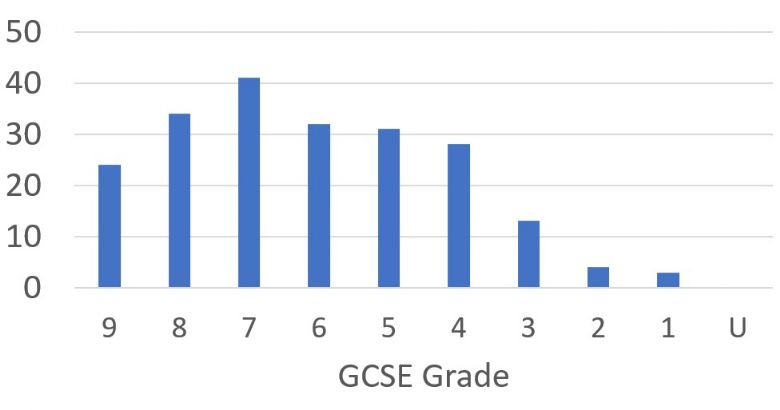
In June 2019, 90.5% of the students in Y11 achieved an 9 - 4 grade in mathematics with 47.1% of pupils gaining a grade 7 or better and 11.4% achieving a grade 9.
| 2019 | 90.5% 9-4 in Maths |
| 2018 | 89.7% |
| 2017 | 94.8% |
| 2016 | 86.1% A*-C in Maths |
| 2015 | 91.3% |
| 2014 | 90.5% |
| 2013 | 93.6% |
| 2012 | 95% |
| 2011 | 90% |
GCSE Mathematics 2019
A level
Advanced level mathematics is growing in popularity and is relevant to most career choices. We offer units in Pure Maths, Mechanics, Statistics and Decision Maths. Balcarras School has an enviable reputation for A Level success.
In 2019, at A Level, 21 students achieved an A* grade and over 80% achieved at least a grade A. This gave the department an ALPS grade 1 making it the best mathematics department in the country (including grammar schools and independent schools). In A Level Further maths 85% achieved at least a grade A. Many of these students went on to study maths at some of the best universities in the country.
- Mathematics was the most applied for subject in the sixth form in 2017, 2018 and 2019
- Balcarras is one of the few schools in the county that offers both A level Mathematics and A level Further Mathematics
What equipment will be needed?
In maths lessons you will need to have a pen, pencil and rubber together with mathematical drawing instruments (e.g. compass, ruler and protractor).
We expect all students to bring and use a scientific calculator and this is essential for two of the examinations papers. The school has mathematical equipment and calculators for sale and these can be purchased from any maths teacher.
- Items of equipment will be on sale during the new Y7 induction meeting in June
- A fixed price pack includes a calculator and all the equipment needed
Does the school take part in any mathematical competitions?
Yes. We regularly enter students for the UKMT Mathematical Challenges at Junior, Intermediate and Senior Levels as well as the regional Team Mathematics Challenges.

We run a maths club for Y11, 12 and 13 pupils every Thursday lunchtime which prepares students for the Maths Challenges and also for STEP/ MAT exams prior to University applications.

